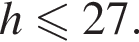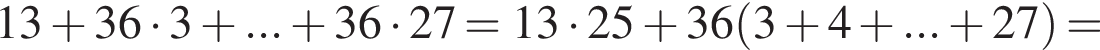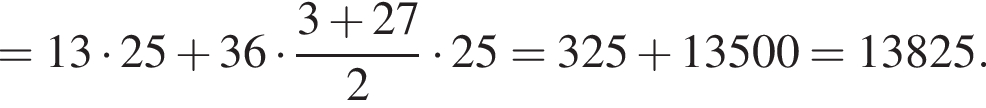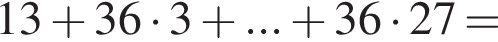Среди точек
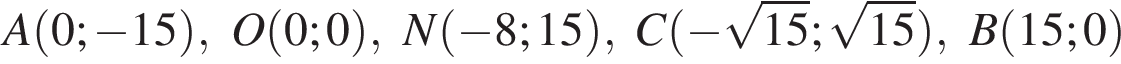 выберите ту, которая принадлежит графику функции, изображённому на рисунке:
выберите ту, которая принадлежит графику функции, изображённому на рисунке:
Точки A, B, C разделили окружность так, что градусные меры дуг AB, BC, CA в указанном порядке находятся в отношении 2 : 9 : 7. Найдите градусную меру угла ABC.
На координатной прямой отмечены точки В(−3), А(8), X(а). Найдите длину отрезка ВХ, если точки В и X симметричны относительно точки А.
Если  то
то  равно:
равно:
Результат упрощения выражения 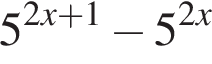 имеет вид:
имеет вид:
Высоты остроугольного равнобедренного треугольника ABC (AB = BC) пересекаются в точке O. Если высота AD = 10 и AO = 6, то длина стороны AC равна:
Площадь параллелограмма равна ![]() его стороны равны 6 и 1. Найдите большую диагональ параллелограмма.
его стороны равны 6 и 1. Найдите большую диагональ параллелограмма.
Результат упрощения выражения 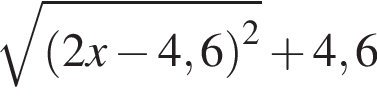 при −1 < x < 1 имеет вид:
при −1 < x < 1 имеет вид:
Свежие фрукты при сушке теряют a % своей массы. Укажите выражение, определяющее массу сухих фруктов (в килограммах), полученных из 60 кг свежих.
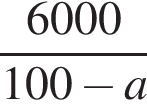
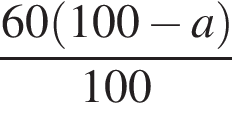
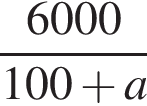
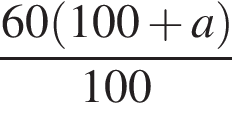
Упростите выражение 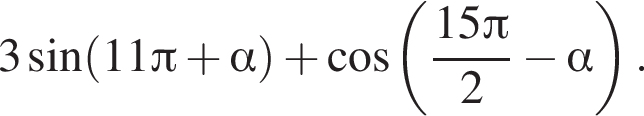
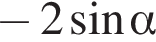


В двух сосудах 57 литров жидкости. Если 5% жидкости из первого сосуда перелить во второй, то в обоих сосудах окажется одинаковое количество жидкости. Сколько литров жидкости было во втором сосуде первоначально?
Для начала каждого из предложений подберите его окончание 1−5 так, чтобы получилось верное утверждение.
A) Значение выражения 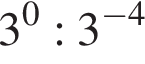 равно:
равно:
Б) Значение выражения 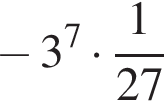 равно:
равно:
В) Значение выражения  равно:
равно:
1) 9
2) −81
3) ![]()
4) ![]()
5) 81
Ответ запишите в виде сочетания букв и цифр, соблюдая алфавитную последовательность букв левого столбца. Помните, что некоторые данные правого столбца могут использоваться несколько раз или не использоваться вообще. Например: А1Б1В4.
Автомобиль проехал некоторое расстояние, израсходовав 21 л топлива. Расход топлива при этом составил 9 л на 100 км пробега. Затем автомобиль существенно увеличил скорость, в результате чего расход топлива вырос до 12 л на 100 км. Сколько литров топлива понадобится автомобилю, чтобы проехать такое же расстояние?
Пусть x0 — корень уравнения 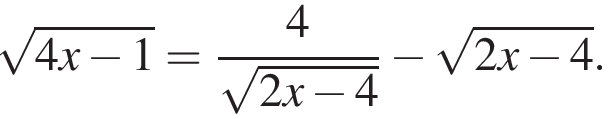 Тогда значение выражения
Тогда значение выражения 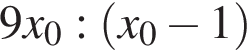 равно ... .
равно ... .
Найдите количество всех целых решений неравенства 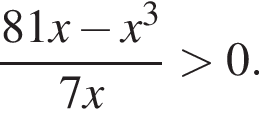
Найдите периметр правильного шестиугольника, меньшая диагональ которого равна ![]()
По двум перпендикулярным прямым, которые пересекаются в точке O, движутся две точки M1 и M2 по направлению к точке O со скоростями 1 ![]() и 2
и 2 ![]() соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 5 м, M2O = 20 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
соответственно. Достигнув точки O, они продолжают свое движение. В первоначальный момент времени M1O = 5 м, M2O = 20 м. Через сколько секунд расстояние между точками M1 и M2 будет минимальным?
Пусть x0 — наибольший корень уравнения 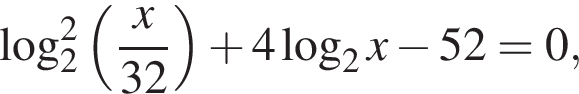 тогда значение выражения
тогда значение выражения ![]() равно ...
равно ...
Найдите произведение наименьшего целого решения на количество всех натуральных решений системы неравенств
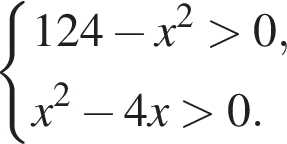
Найдите площадь боковой поверхности правильной треугольной пирамиды, если длина биссектрисы ее основания равна ![]() и плоский угол при вершине
и плоский угол при вершине 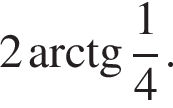
Найдите (в градусах) наибольший отрицательный корень уравнения 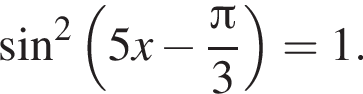
Верхнюю сторону листа фанеры прямоугольной формы разделили для покраски прямой линией на две части так, как показано на рисунке. Треугольную часть (I) покрасили краской белого цвета, а четырехугольную (II) — краской серого цвета. Сколько серой краски (в граммах) было использовано, если краски белого цвета понадобилось 280 г и расход краски (г/см2) обоих цветов одинаков?
Найдите значение выражения 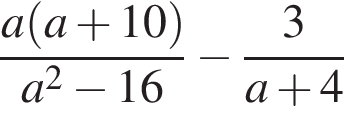 при
при 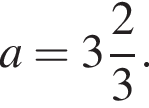
Три числа составляют геометрическую прогрессию, в которой ![]() Если второй член прогрессии уменьшить на 10, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 36, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Если второй член прогрессии уменьшить на 10, то полученные три числа в том же порядке опять составят геометрическую прогрессию. Если третий член новой прогрессии уменьшить на 36, то полученные числа составят арифметическую прогрессию. Найдите сумму исходных чисел.
Найдите сумму целых значений x, принадлежащих области определения функции
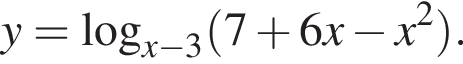
Найдите увеличенную в 25 раз сумму квадратов корней уравнения
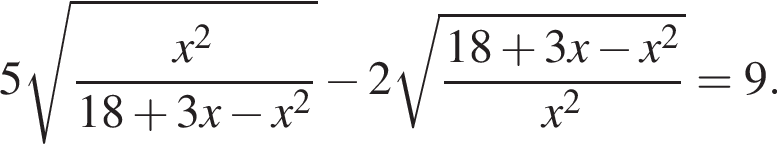
Из точки А проведены к окружности радиусом 4 касательная AB (B — точка касания) и секущая, проходящая через центр окружности и пересекающая ее в точках D и C (AD < AC). Найдите площадь S треугольника ABC, если длина отрезка AC в 3 раза больше длины отрезка касательной. В ответ запишите значение выражения 5S.
Количество целых решений неравенства 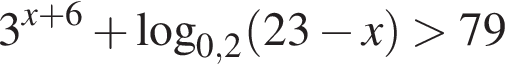 равно ...
равно ...
ABCDA1B1C1D1 — куб. Точка K лежит на ребре AB куба так, что AK : KB = 2 : 1. Найдите значение выражения 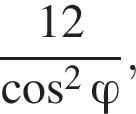 где φ — угол между прямыми A1K и B1D1.
где φ — угол между прямыми A1K и B1D1.
Найдите сумму всех трехзначных чисел, которые при делении на 4 и на 6 дают в остатке 1, а при делении на 9 дают в остатке 4.

 представляет собой прямую, проходящую через точки вида
представляет собой прямую, проходящую через точки вида 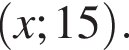 Таким образом, единственное подходящее решение — точка N.
Таким образом, единственное подходящее решение — точка N.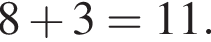 Тогда длина BX равна
Тогда длина BX равна 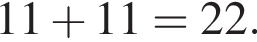
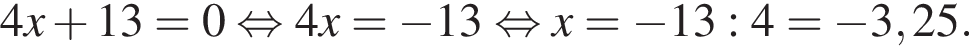



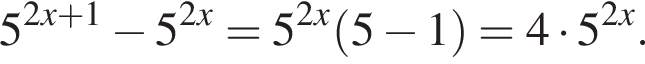
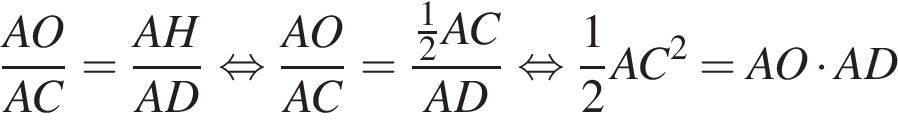
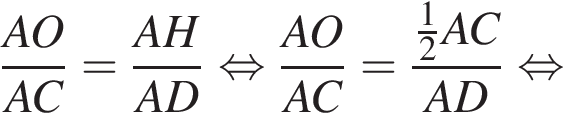
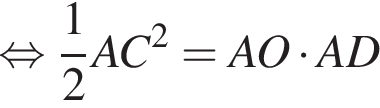


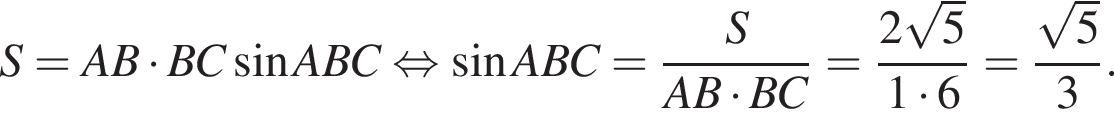

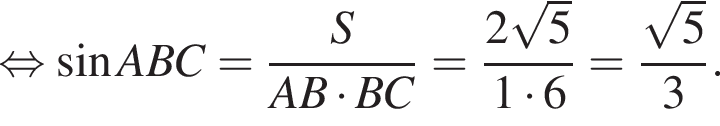
 заметив, что угол ABC тупой:
заметив, что угол ABC тупой: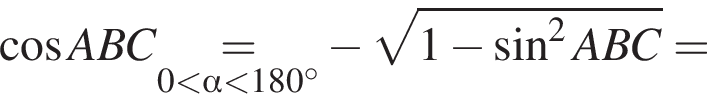
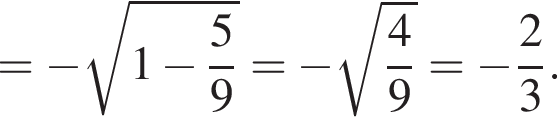
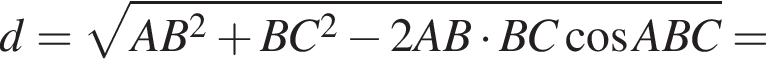
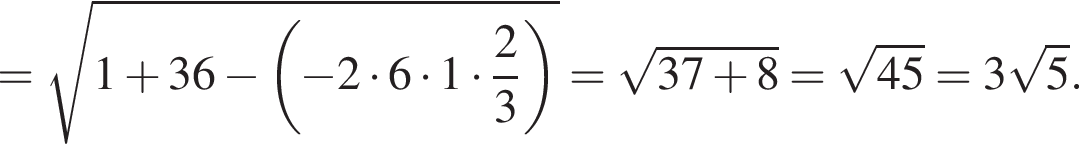
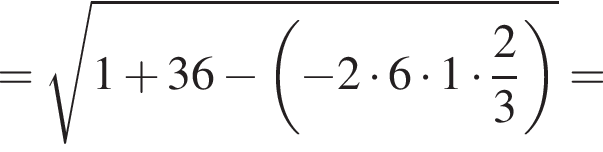


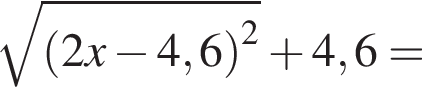
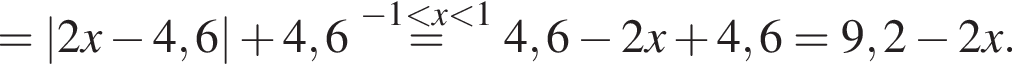
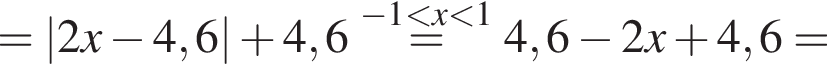
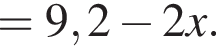
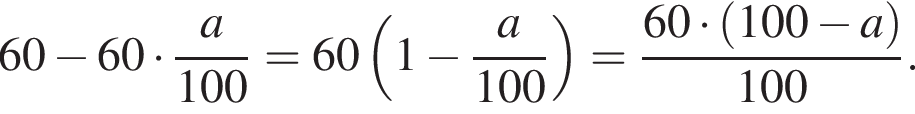

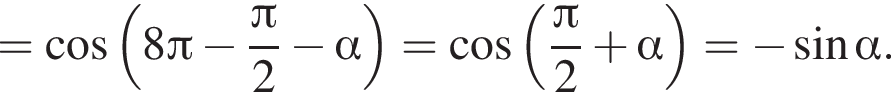
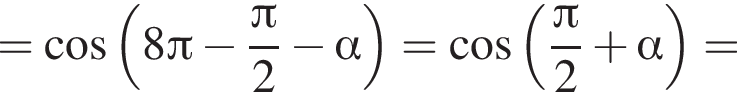
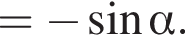
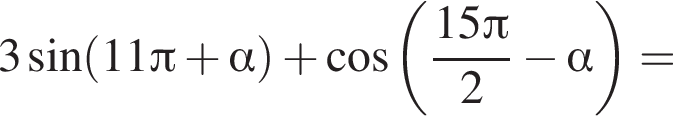

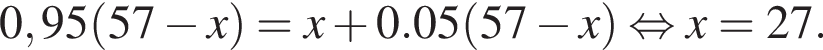


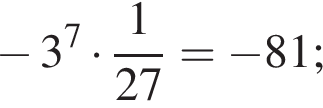
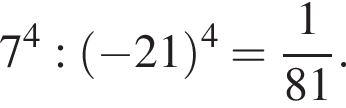
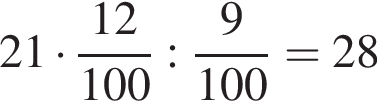 л.
л.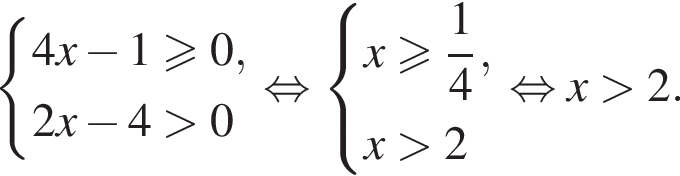
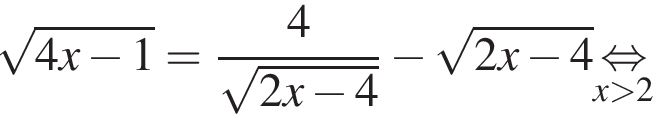
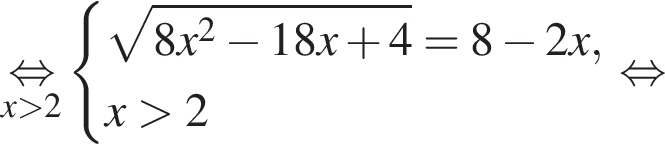
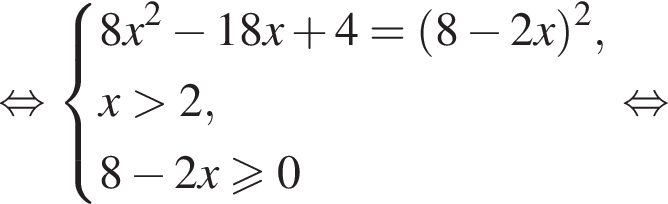
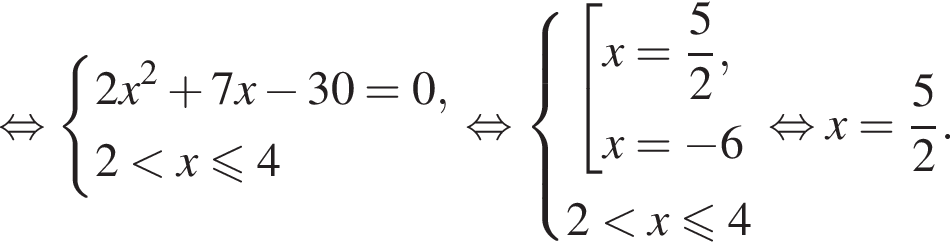
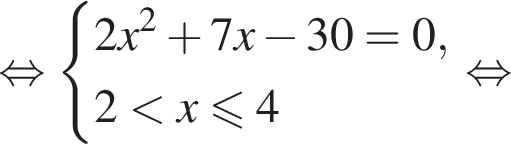
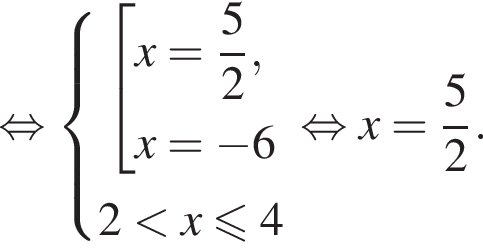
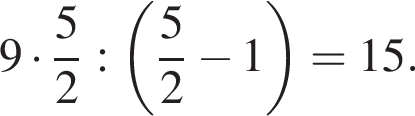
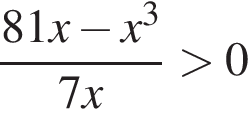
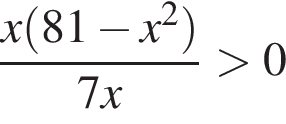
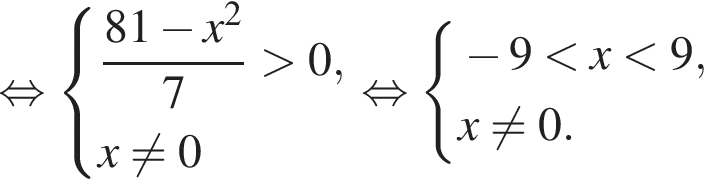
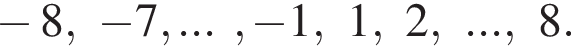
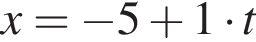 (м) и
(м) и 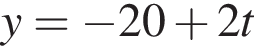 (м).
(м).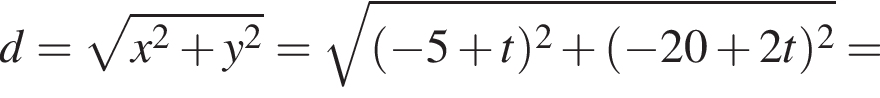
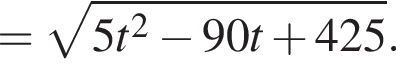
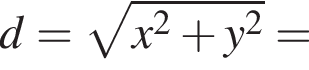
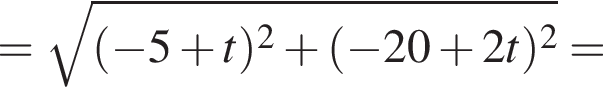
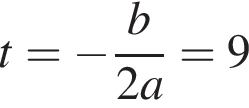 и в этой точке положительно:
и в этой точке положительно: 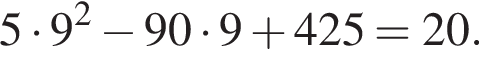 Таким образом, при
Таким образом, при 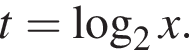
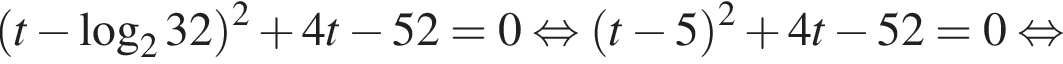
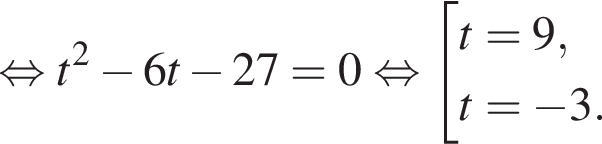
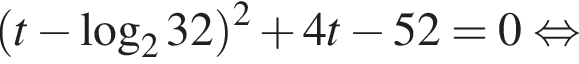
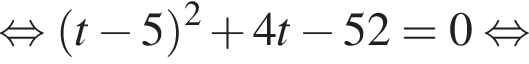
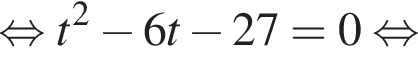
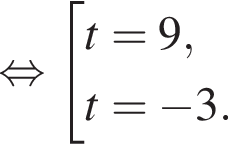
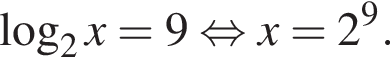 Тогда
Тогда 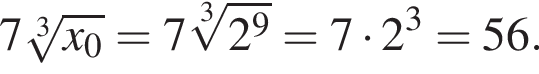
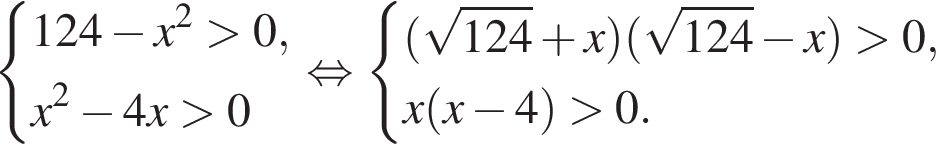
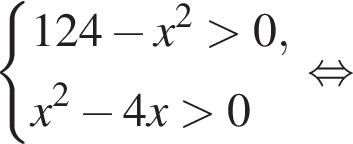
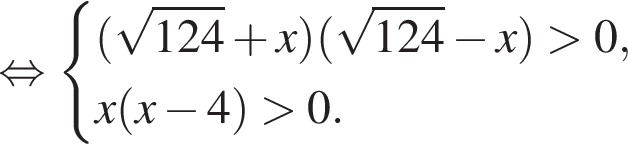
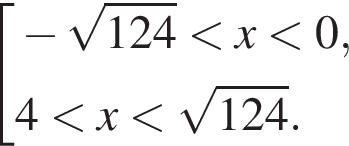
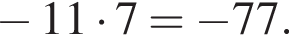
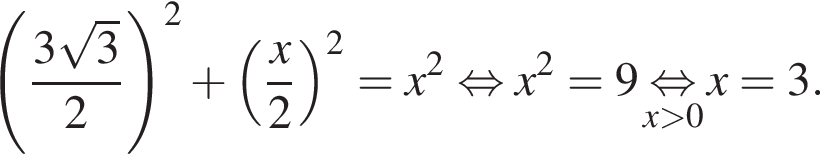
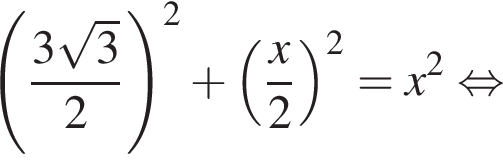
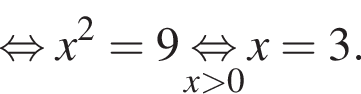
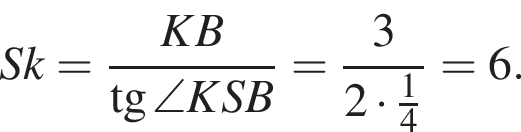
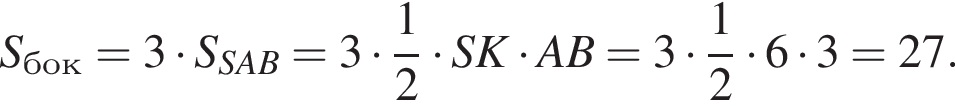
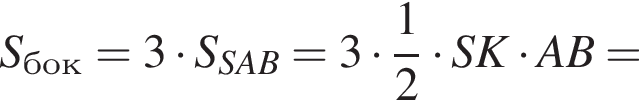
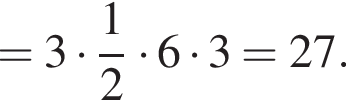
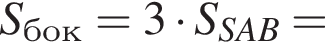
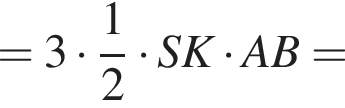
 :
: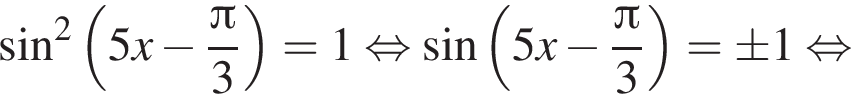
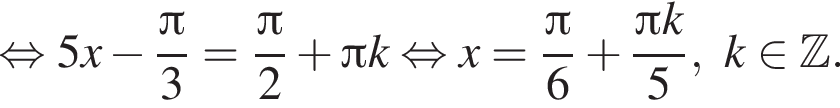
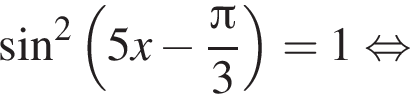
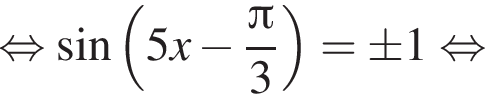
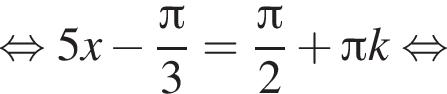
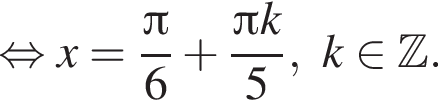
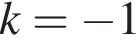 и равен
и равен 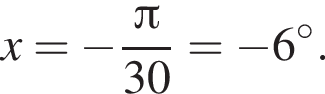
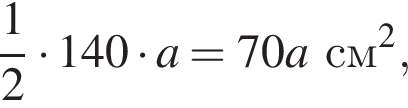 а расход краски равен
а расход краски равен 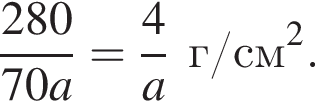 Площадь четырехугольной части листа равна
Площадь четырехугольной части листа равна 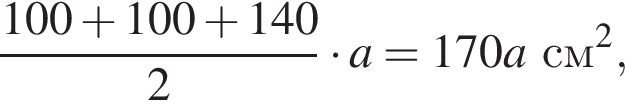
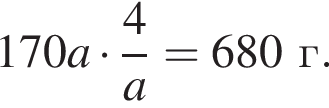
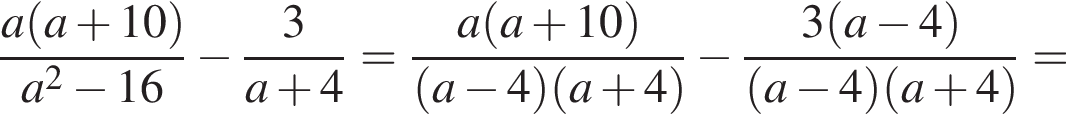
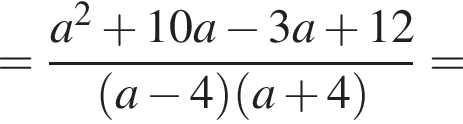
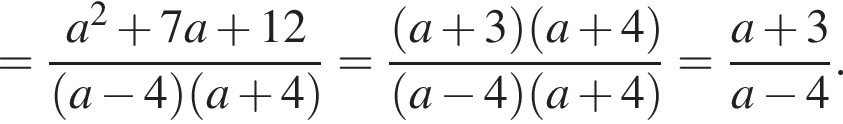
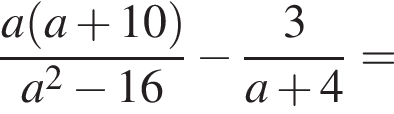
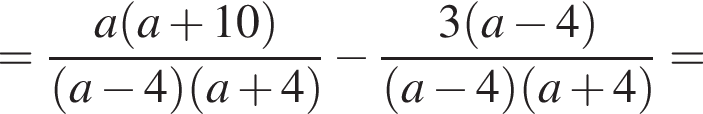
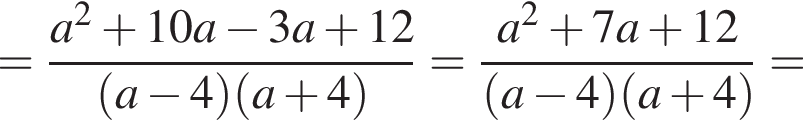
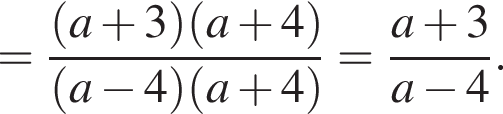
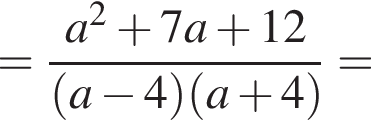
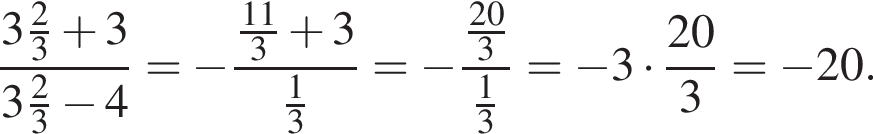
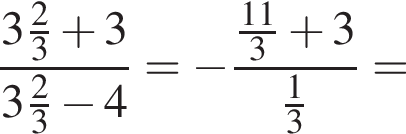
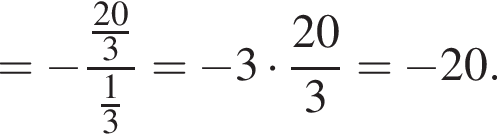
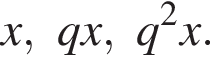
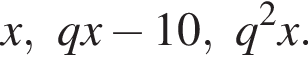
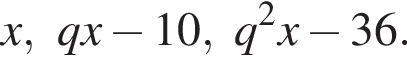
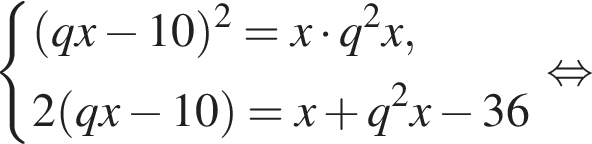
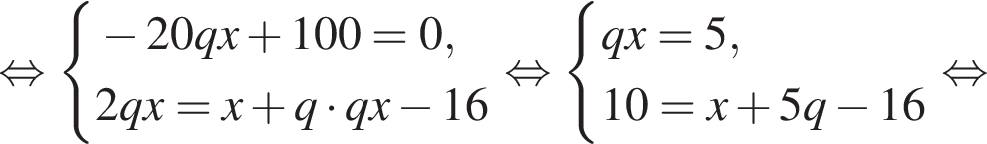
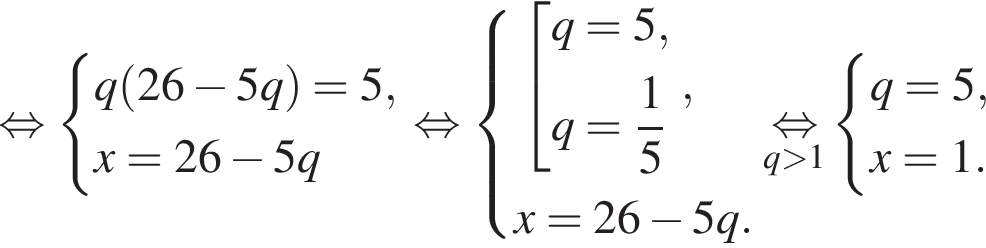
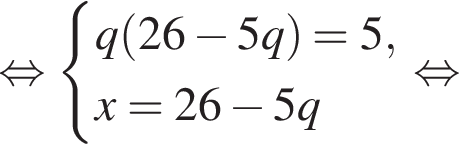
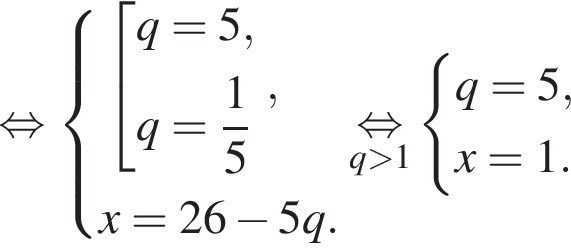
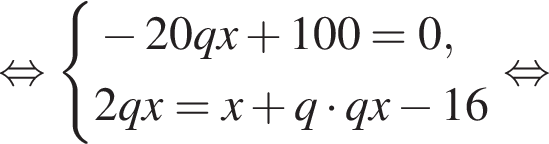
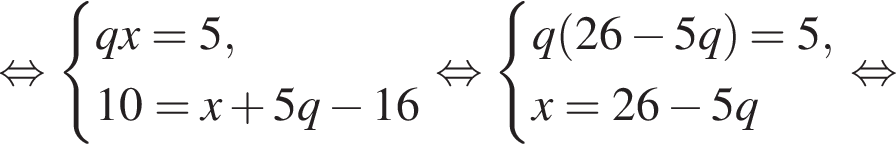
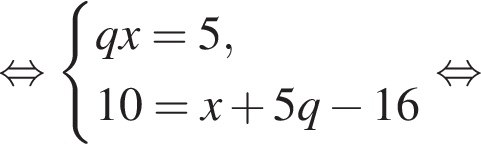
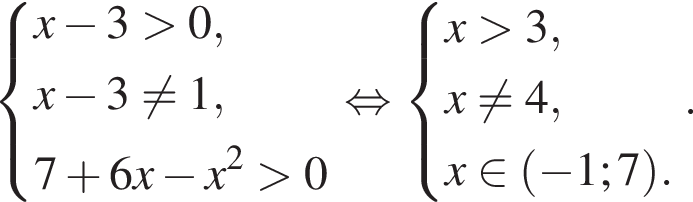
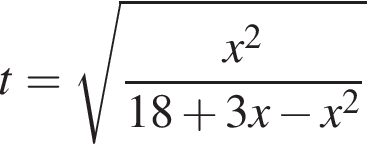 при
при 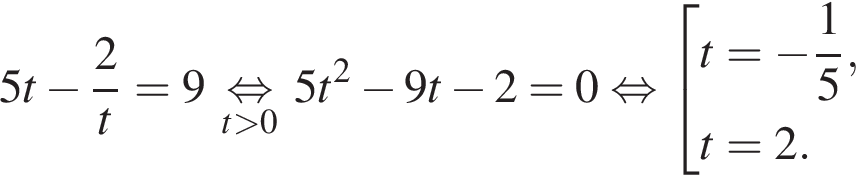
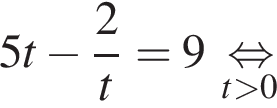
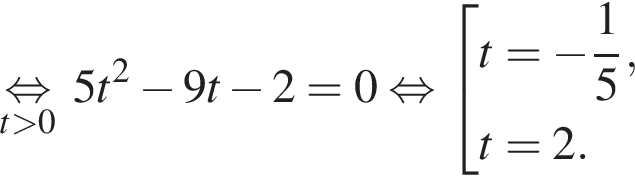
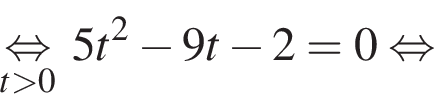
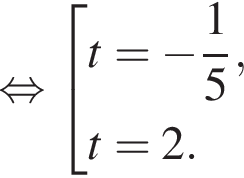
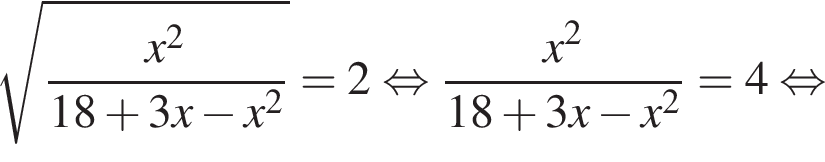
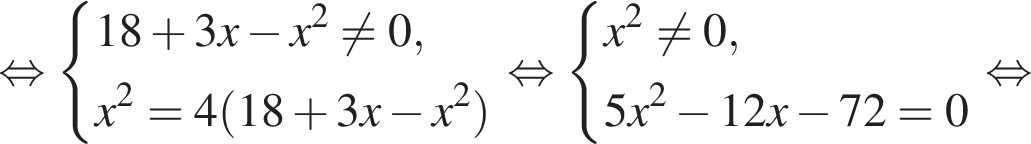
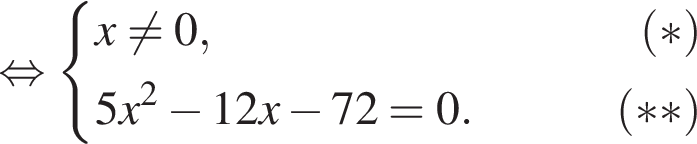
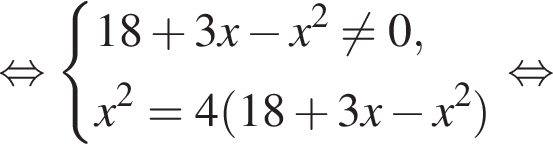
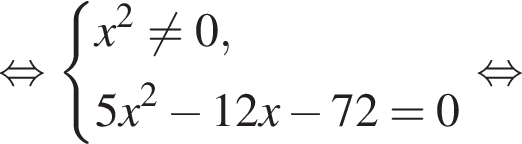
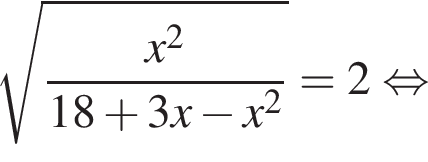
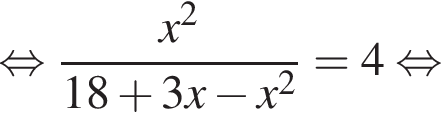
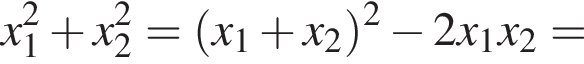
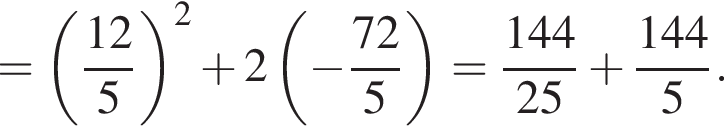
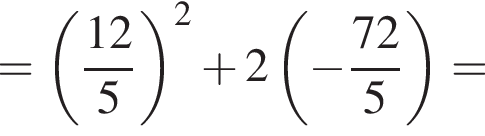
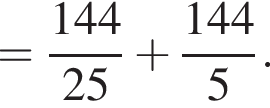
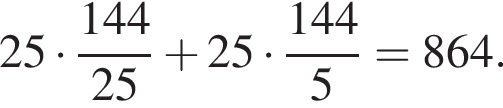
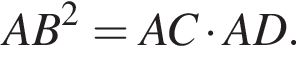 Обозначим AB за x, тогда
Обозначим AB за x, тогда  Тогда:
Тогда: 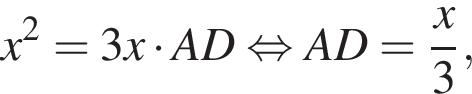 при этом
при этом 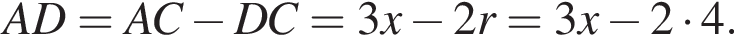 Получим:
Получим: 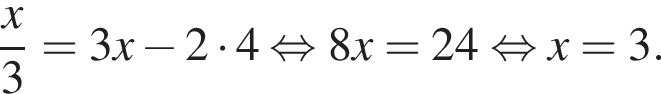
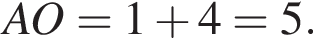
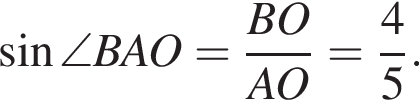 Тогда площадь треугольника ABC:
Тогда площадь треугольника ABC: 
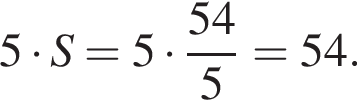
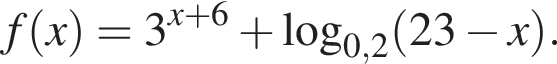 Заметим, что по смыслу задачи
Заметим, что по смыслу задачи 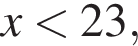 и что на
и что на 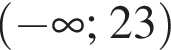
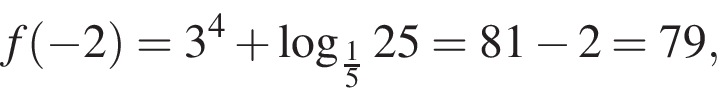 неравенство верно для всех x из
неравенство верно для всех x из 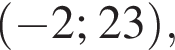 который содержит 24 целых числа.
который содержит 24 целых числа.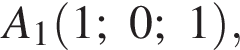
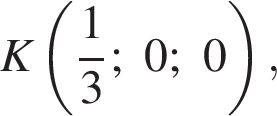
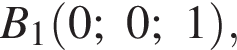
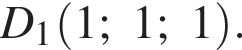 Найдем координаты вектора
Найдем координаты вектора 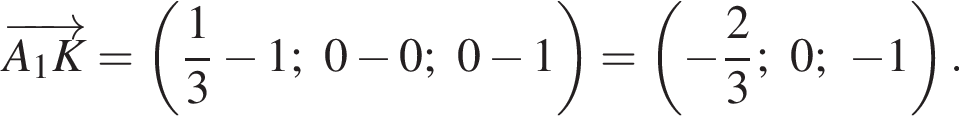
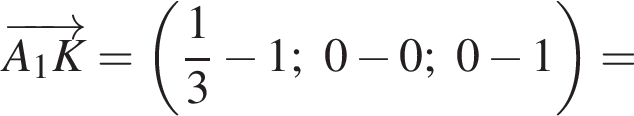
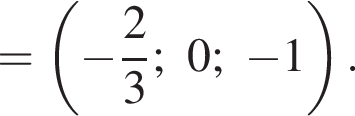
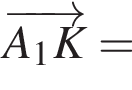
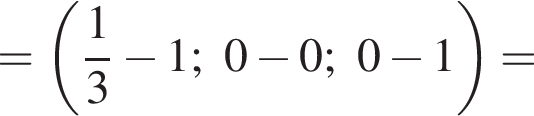
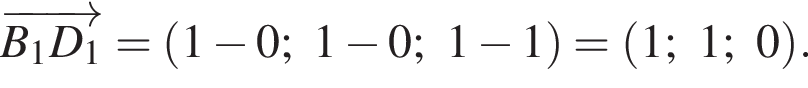
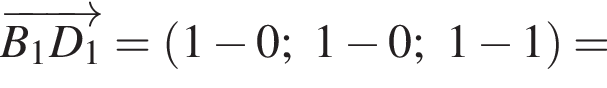
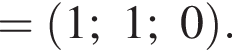
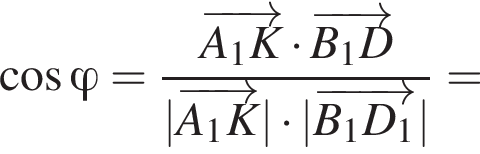
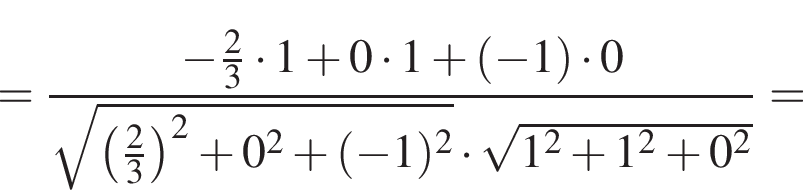
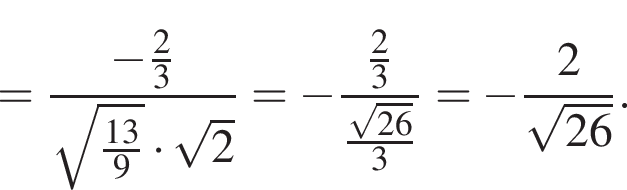
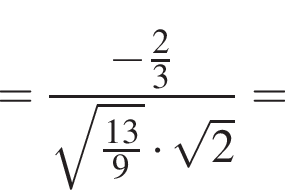
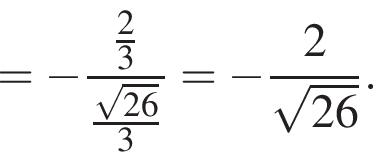
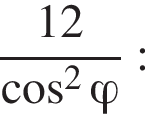
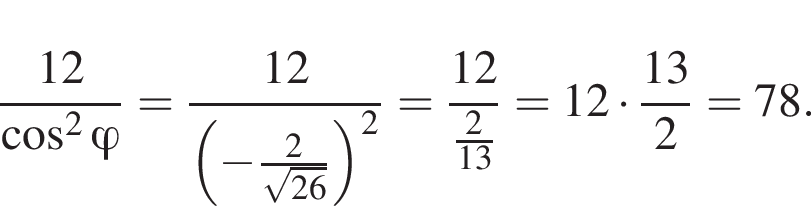
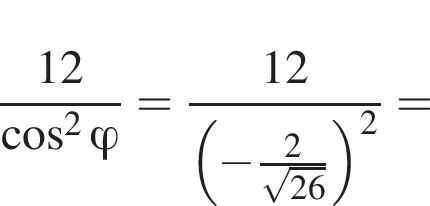
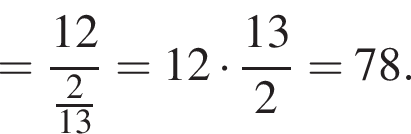
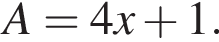


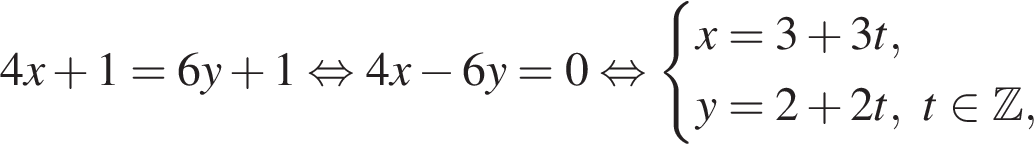
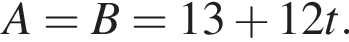
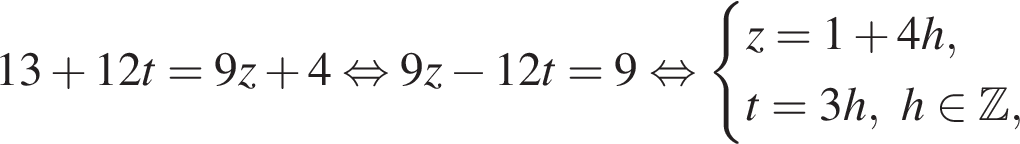

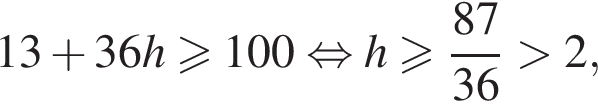 h — целое, поэтому
h — целое, поэтому  h — целое, поэтому
h — целое, поэтому